Course Computational Mathematics

Bisection Method

In this lesson, we'll talk about the Bisection Method and some applications of it. To understand how it works, consider the following problem:

Given a function and an interval such that and have opposite signs (that is, and or and ), check if has a root in this interval. If it has, find one of them

Before we solve the problem, let's analyze some properties of the problem.

Continuous Functions

The first important property is that is continuous. The exact definition of continuous function involves some complicated topics in mathematics, but looking at the graphic of this concept is very intuitive.

A function is continuous if and only if we can draw its graphic without taking the pencil out of the paper

Let's look at some examples.

Figure 1 : This is the graph of the function g(x) = x - 3 and it is continuous because we can draw it without taking the pencil out of the paper

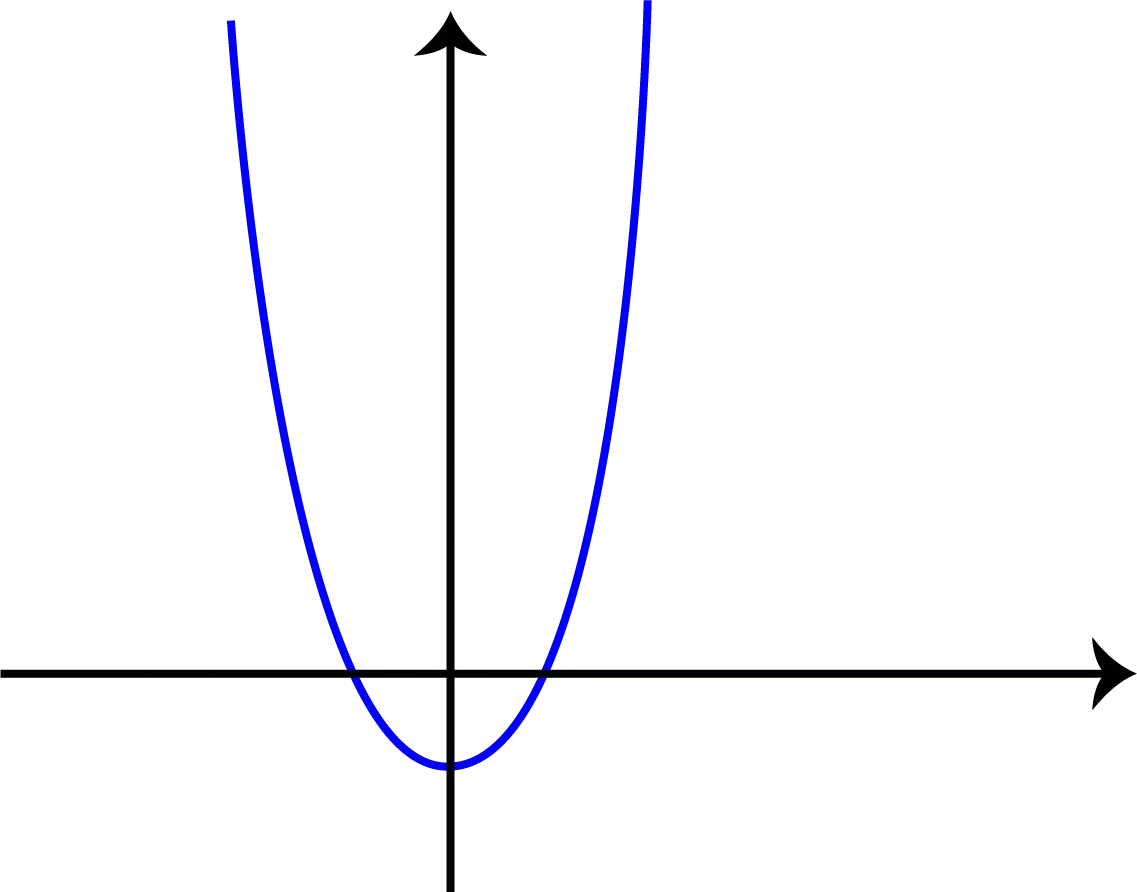
Figure 2 : this is the graph of the function h(x) = x*x - 1 and it is continuous because we can draw it without taking the pencil out of the paper

Figure 3 : This is the graph of the function i(x) = 1/x and it is not continuous because it is divided into two separate parts

Get a PRO Subscription and unlock this lesson